物理信息径向基网络

参考 Physics-informed radial basis network (PIRBN): A local approximating neural network for solving nonlinear partial differential equations

特点：

• 单个隐藏层，使用径向基函数作为激活函数
• PIRBN 收敛到高斯过程
• NTK 理论分析 PINN 在训练完成时表现出局部逼近性质，而 PIRBN 在整个训练过程中都有这种局部性质
• 适用于含有高频特征的问题

常微分方程求解

考虑下面的常微分方程：

$${\displaystyle \frac{\mathrm{d}u}{\mathrm{d}x}}=50\cos (50x),u(0)=0,x\in [0,6]$$

该方程的真实解为 $u(x)=\sin (50x)$, 其中含有一个高频率特征。现在考虑使用 PIRBN 对其进行求解。

步骤 1 导入模型

导入必要的库

import torch
import nets
mdl = nets.PIRBN([1,201,1],extent=[-0.5,6.5])

上面的语句可以方便的构建一个 PIRBN, 其中 [1,201,1] 的含义是：

• 1：输入神经元的数量为 1，对应问题的自变量 $x$
• 201： 第一个隐藏层的神经元数量为 201
• 1：输出神经元的数量为 1，对应问题的 $u(x)$

因为 PIRBN 要求网络是单层的，所以下面的操作是无效的：

mdl = nets.PIRBN([1,201,201,1])

在创建 PIRBN 时还需要给定一个区间 extent，这个区间是径向基函数中心的采样区间，该区间要求能够覆盖住我们的求解区间。如本例，我们的求解区间为 $[0,6]$，所以我们选择一个能够覆盖它的 extent=[-0.5,6.5]

步骤 2 翻译

将求解问题翻译成代码。这个问题涉及一阶导数，我们可以使用下面命令来指定我们需要的导数：

mdl.set_diff_chain("u_1")

其中 "u_" 是固定前缀，"1" 代表对第一个自变量求导 1 次，即 $u_x$，如果我们想要得到 $u_{xx}$ 和 $u_{yy}$，则可以

mdl.set_diff_chain("u_11","u_22")

"11" 代表对第一个自变量求导 2 次，即 $u_{xx}$，"22" 代表对第二个自变量求导 2 次。

我们需要定义一个 conditions 函数，在该函数中返回每一个条件的残差：

x0 = torch.tensor([[0.]])
u0 = torch.tensor([[0.]])
def conditions(x,u,du):
    f1 = du["u_1"] - 50*torch.cos(50*x)
    f2 = mdl(x0) - u0
    return f1, f2

这里 conditions 接收三个参数，x, u, du, 分别代表：

• x, 神经网络的输入
• u, 神经网络的输出
• du, 神经网络输出对输入的各种导数的集合，由 mdl.set_diff_chain 语句确定

在 conditions 内部我们返回了两个残差，他们分别是：

• f1, 对应方程条件的残差
• f2, 对应初始条件的残差

步骤 3 传条件

将翻译好的条件传给 PIRBN。

mdl.conditions = conditions

步骤 4 训练

选择配置，进行训练。我们的训练函数是 pde_solve，当我们调出这个函数时，编辑器会自动弹出一份文档，里面有可参考的配置信息，我们也可以直接复制：

x = torch.linspace(0,6,1000,requires_grad=True).view(-1,1)
sets = {
    "x": x,
    "optimizer": torch.optim.LBFGS,
    "lr": 1,
    "epochs": 100,
}
mdl.pde_solve(**sets)

这里的 x 是用于训练的数据点，对应我们本例问题自变量 $x$ 在区域 $[0,6]$ 的采样。在这个配置单（sets,名称可修改）中，我们指定了采样点，指定优化器（优化算法）为 LBFGS 算法，学习了为 1，迭代次数 100 次。使用 mdl.pde_solve(**sets) 就可以训练了。

步骤 5 可视化

可视化。训练结束后，我们可以使用 predict 函数对求解区间的任意点进行预测，一个简单的可视化代码如下：

import matplotlib.pyplot as plt

def plot(mdl):
    t = torch.linspace(0,6,1000).view(-1,1)
    plt.plot(t,torch.sin(50*t))
    plt.plot(t,mdl.predict(t))

plot(mdl)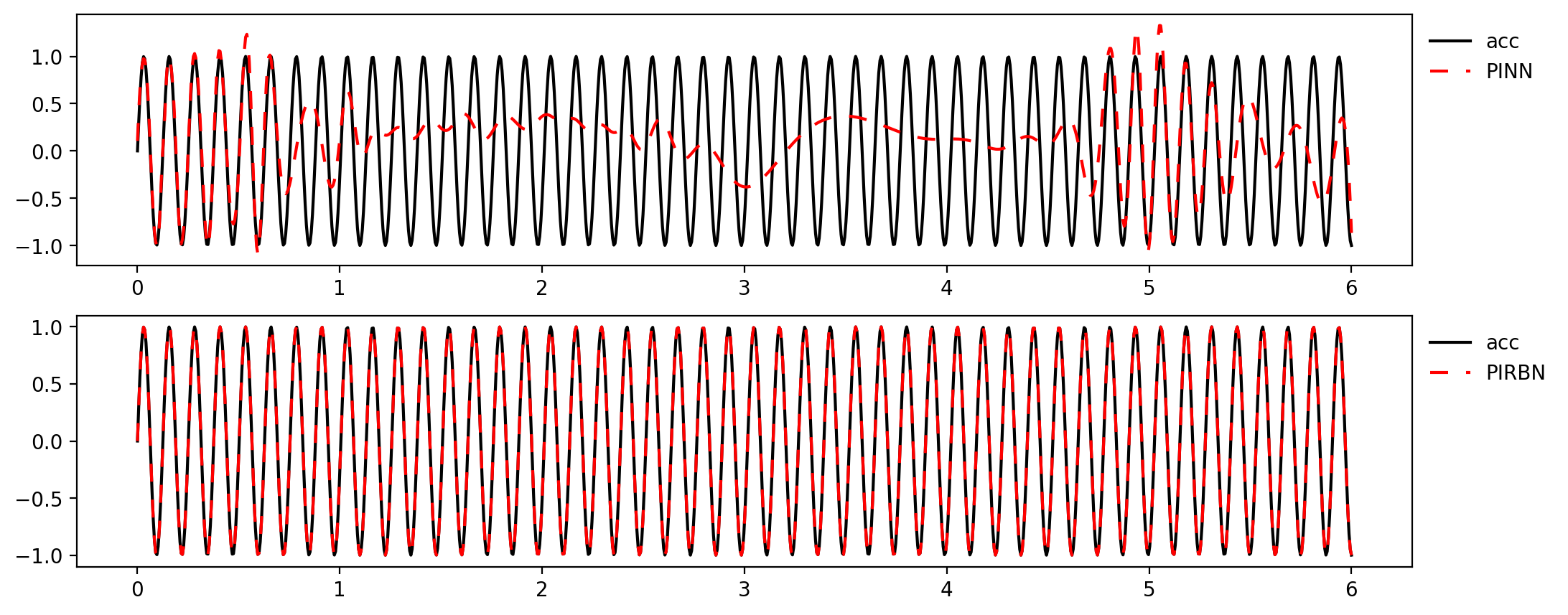

偏微分方程求解

考虑如下波动方程：

$$\begin{array}{rl}& (\frac{{\partial }^2}{\partial x^2}-4\frac{{\partial }^2}{\partial y^2})u(x,y)=0,\mathrm{for}x\in [0,1],y\in [0,1],\\ & u(x,0)=u(x,1)=\frac{\partial }{\partial x}u(0,y)=0,\\ & u(0,y)=\sin (\pi y)+\frac{1}{2}\sin (4\pi y).\end{array}$$

其真实解为

$$u(x,y)=\cos (2\pi x)\sin (\pi y)+\frac{1}{2}\cos (8\pi x)\sin (4\pi y).$$

现考虑使用 PIRBN 对其求解。

步骤 1 导入模型

import torch
import nets
import myfuntools as mft
mdl = nets.PIRBN([2,21,1],extent=[-0.1,1.1]*2)

该语句可以方便地创建一个 PIRBN, 与常微分情况类似，这个我们传入一个 extent=[-0.1,1.1]*2 来覆盖我们的求解区域 $[0,1{]}^2$. 径向基函数的中心将在这个区域内均匀取值

步骤 2 翻译

将求解问题翻译成代码。我们需要在 conditions 函数中返回每个条件的残差。这个问题在求解区域内涉及两个二阶导数，我们可以使用下面命令来指定我们需要的导数：

mdl.set_diff_chain("u_11","u_22")

"11" 代表对第一个自变量求导 2 次，即 $u_{xx}$，"22" 代表对第二个自变量求导 2 次, 即 $u_{yy}$

创建区域内和边界上的样点：

be = mft.creat_ereadata(0,1,0,1,500).requires_grad_(True)
oy = mft.creat_ereadata(0,0,0,1,50)
oyg = oy.clone().requires_grad_(True)
x0 = mft.creat_ereadata(0,1,0,0,50)
x1 = mft.creat_ereadata(0,1,1,1,50)

根据条件给出残差：

def conditions(x,u,du):
    f1 = du["u_11"] - 4*du["u_22"]
    f2 = mdl(x0)
    f3 = mdl(x1)
    f4 = torch.autograd.grad(mdl(oyg),oyg,torch.ones(50,1),create_graph=True,retain_graph=True)[0][:,0:1]
    f5 = mdl(oy) - torch.sin(torch.pi*oy[:,1:2])- torch.sin(4*torch.pi*oy[:,1:2])/2
    return f1, f2, f3, f4, f5

步骤 3 传条件

将翻译好的条件传给 PIRBN。

mdl.conditions = conditions

步骤 4 训练

选择配置，进行训练。我们的训练函数是 pde_solve，当我们调出这个函数时，编辑器会自动弹出一份文档，里面有可参考的配置信息，我们也可以直接复制：

sets = {
    "x": be,
    "optimizer": torch.optim.LBFGS,
    "lr": 1,
    "epochs": 100,
}
mdl.pde_solve(**sets)

步骤 5 可视化

可视化。

import matplotlib.pyplot as plt

def myplot(mdl):
    t1 = torch.linspace(0, 1, 90).view(1, -1)
    t2 = torch.linspace(0, 1, 100).view(-1, 1)
    acc = torch.cos(2*torch.pi*t1)*torch.sin(torch.pi*t2) + torch.cos(8*torch.pi*t1)*torch.sin(4*torch.pi*t2)/2

    shape = (t1 + t2).shape
    p1 = t1.broadcast_to(shape)
    p2 = t2.broadcast_to(shape)
    pe = torch.cat((p1.flatten().view(-1, 1), p2.flatten().view(-1, 1)), dim=1)
    pre = mdl.predict(pe)

    fig = plt.figure(figsize=(12, 3))
    ax1 = fig.add_subplot(1, 3, 1)
    im1 = ax1.imshow(acc, extent=[0, 1, 0, 1], origin="lower")
    plt.colorbar(im1)

    ax2 = fig.add_subplot(1, 3, 2)
    im2 = ax2.imshow(pre.view_as(acc), extent=[0, 1, 0, 1], origin="lower")
    plt.colorbar(im2)

    ax3 = fig.add_subplot(1, 3, 3)
    im3 = ax3.imshow(abs(pre.view_as(acc) - acc), extent=[0, 1, 0, 1], origin="lower")
    plt.colorbar(im3)
    plt.tight_layout()

myplot(mdl2)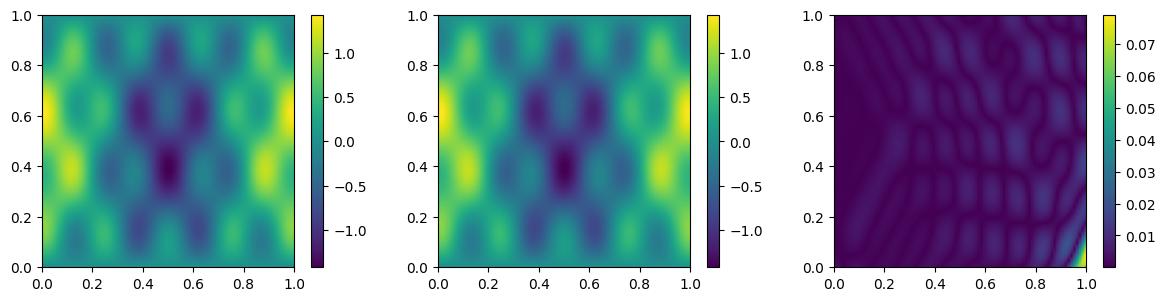

从左到右依次是精确值、预测值、逐点绝对误差。

TIP

该结果并非训练 100 得到，而是经过了长时间的训练。在原论文中，作者用 Adam 训练，给出的 epochs 为 8000 次，我们严格按作者的配置也没能重现论文中的精度。而作者所给出的图像上面却写着训练 8 万次。我们猜测，真实的训练次数为 8 万而非 8 千。